Symulacja silnika prądu stałego w SPICE
Ostatnio pomagając stażystom pracującym nad budową robota mobilnego stwierdziliśmy, że przy takiej pracy przydałaby się możliwość numerycznej symulacji pracy układu sterowania silnikiem. Najlepiej gdyby dało się to zrobić przy pomocy któregoś ze standardowych programów typu SPICE (ja bardzo lubię darmowego LTSpice’a). Niestety silnik DC jest elementem, którego właściwości elektryczne są ściśle związane z właściwościami mechanicznymi np. prędkością obrotową czy tarciem. Nie da się tych wielkości modelować bezpośrednio w wielu popularnych symulatorach. Na szczeście przy odrobinie pomysłowości i znajomości fizyki można ten problem łatwo obejść.
Plik z obwodem do symulacji silnika w programie LTSpice, który opisuję w tym wpisie możesz znaleźć pod tym linkiem.
Zjawiska fizyczne w silniku prądu stałego
Na początek musimy sobie wyjaśnić kilka zjawisk, które zachodzą w silnikach prądu stałego. Nie będę tutaj opisywał zbyt dokładnie ogólnej zasady działania takiego silnika – można znaleźć te informacje w wielu miejscach w sieci. Skupimy się za to na mniej rozumianych efektach, które są istotne dla symulacji zachowania naszego silnika przy pomocy programów typu SPICE. Bedą to:
- Generacja momentu siły obracającego wirnik.
- Generacja wstecznej siły elektromotorycznej.
- Opory ruchu.
Generacja momentu obrotowego
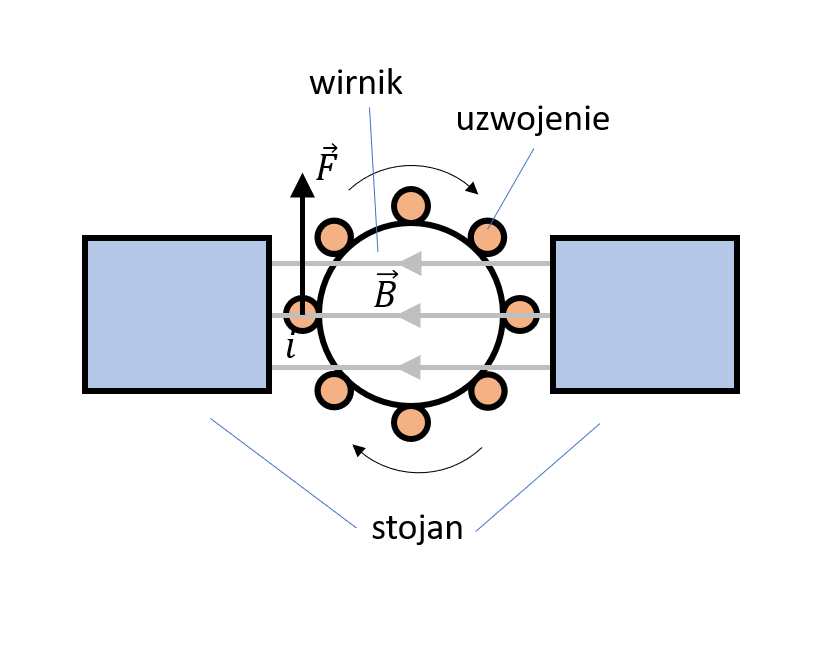
Uproszczony schemat silnika prądu stałego widzisz na rys. 1. Ogólna zasada działania jest dość prosta. Przez uzwojenie wirnika przepływa prąd elektryczny. Ponieważ uzwojenie to jest umieszczone w polu magnetycznym utworzonym przez stojan to zgodnie z prawami fizyki na zwoje zacznie działać siła o wartości $F=Bil$, gdzie $B$ to indukcja pola magnetycznego, $i$ – natężenie prądu płynącego przez uzwojenie, a $l$ długość zwojów.
Siła ta jest prostopadła zarówno do wektora indukcji pola magnetycznego jak i przewodów w uzwojeniu. Jej kierunek widzisz zaznaczony na rysunku. Oczywiście tak skierowana siła zacznie obracać wirnik. Dla nas ważna będzie dalej wartość momentu obrotowego: $T=Fd$, gdzie $d$ to odległość od miejsca działania siły do osi obrotu wirnika. Oczywiście całkowity moment obrotowy jest sumą momentów działających na każdy zwój z osobna.
Ważne jest, że moment obrotowy jest proporcjonalny do płynącego przez uzwojenie prądu. Możemy to zapisać za pomocą wzoru:
$$T = k_1i,$$
gdzie $k_1$ to stała charakterystyczna dla konkretnego silnika. Jest ona wyrażona w $Nm/A$ (niutonometrach na amper) i proporcjonalna do: indukcji pola magnetycznego, ilości i długości zwojów oraz średnicy wirnika.
Druga zasada dynamiki dla silnika
Moment obrotowy wytwarza przyspieszenie kątowe. Korzystając drugiej zasady dynamiki możemy zapisać:
$$\frac {d\omega}{dt} = \frac{T}{I},$$
gdzie $\omega$ to prędkość kątowa (w radianach na sekundę), a $I$ – moment bezwładności wirnika i ewentualnych dołączonych do niego elementów.
Równanie $\frac {d\omega}{dt} = \frac{T}{I}$ mówi nam, że prędkość kątowa wirnika zwiększa się w tempie proporcjonalnym do momentu obrotowego i odwrotnie proporcjonalnym do momentu bezwładności wirnika. Jest to równanie opisujące działanie części mechanicznej silnika. W programach typu SPICE nie ma bezpośredniej możliwości umieszczania modeli elementów mechanicznych, ale mamy do dyspozycji modele elementów elektrycznych, których działanie opisuje się identycznymi równaniami.
Np. pracę kondensatora opisuje równanie:
$$\frac{du}{dt} = \frac{i}{C},$$
gdzie $u$ to napięcie na kondensatorze, $i$ – płynący przez niego prąd, a $C$ – pojemność. Zwróć uwagę, że jeżeli zastąpimy $u$ przez $\omega$, $i$ przez $T$, a $C$ przez $I$ to otrzymamy równanie opisujące ruch wirnika. Będzie to dla nas niedługo bardzo przydatne.
Generacja wstecznej siły elektromotorycznej
Po podłączeniu uzwojenia wirnika do napięcia stałego płynie przez nie stały prąd. Wynikałoby z tego, że silnik wciąż by przyspieszał. W praktyce silniki prądu stałego tak się jednak nie zachowują.
Zaraz po podłączeniu napięcia zasilania przez uzwojenie płynie bardzo duży prąd, który później maleje, a silnik przestaje przyspieszać.
Za ten efekt odpowiedzialna jest tzw. wsteczna siła elektromotoryczna. Na czym to polega?
Z prawa Faradaya wynika, że jeżeli pętla z prądem znajduje się w zmiennym polu magnetycznym to pojawi się w niej siła elektromotoryczna, która zachowuje się tak jak dodatkowe dołączone do tej pętli źródło napięcia. Siła te będzie proporcjonalna do szybkości zmian strumienia pola magnetycznego przechodzącego przez pętlę.
Ponieważ wirnik silnika to tak właściwie dużo takich pętli umieszczonych w polu magnetycznym, to gdy wirnik zacznie się poruszać, pojawi się na nim siła elektromotoryczna. W związku z tym możemy zamodelować taki wirnik jako trzy połączone szeregowo elementy:
- Rezystor modelujący rezystancję wirnika.
- Cewkę indukcyjną (wirnik wytwarza też własne pole magnetyczne).
- Źródło napięcia, które modeluje właśnie siłę elektromotoryczną.
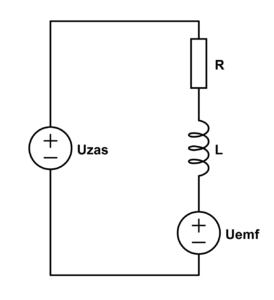
Taki model silnika jest pokazany na rys. 2. Zwróć uwagę zwłaszcza na kierunek dodatkowego źródła napięcia. Jest ono skierowane tak, że przeciwdziała napięciu zasilania.
Co z tego wynika? Na początek zapiszmy równanie mówiące, że siła elektromotoryczna jest proporcjonalna do prędkości wirnika (im szybciej obraca się silnik tym będzie większa):
$$U_{EMF} = k_2 \omega,$$
gdzie $k_2$ to kolejny charakterystyczny parametr silnika mierzony w $V/rad/s$ (woltach na radian na sekundę).
Im szybciej obraca się wirnik tym mniejszy będzie płynął przez niego prąd ponieważ wsteczna siła elektromotoryczna „wygasza” napięcie zasilania.
W pewnym momencie siła elektromotoryczna będzie równa napięciu zasilania. Wtedy przez wirnik przestanie płynąć prąd i moment obrotowy też całkowicie zniknie.
Opory ruchu
Doszliśmy do wniosku, że idealny silnik rozpędzałby się do prędkości obrotowej równej $U_{zas}/k_2$, a potem przestałby przez niego płynąć prąd, a prędkość obrotowa by się ustabilizowała.
To oczywiście też nie jest zachowanie, które występuje w rzeczywistych silnikach. W stanie ustalonym przez silnik płynie niezerowy (a czasem nawet dość spory) prąd.
Jest to spowodowane oporami ruchu. Kiedy wirnik się obraca to różne zjawiska powodują powstanie dodatkowego momentu hamującego. Moment ten jest proporcjonalny do prędkości obrotowej wirnika:
$$T_h = \beta \omega,$$
gdzie $\beta$ to współczynnik oporu wyrażony w $Nm/rad/s$ (niutonometrach na radian na sekundę).
W stanie ustalonym, gdy silnik porusza się ze stałą prędkością, musi wytwarzać moment obrotowy równoważący moment hamujący. Wymaga to przepływu pewnego prądu. Oznacza to, że wsteczna siła elektromotoryczna nigdy nie dojdzie do wartości $U_{zas}$, a silnik nigdy nie rozpędzi się do prędkości $\omega = U_{zas}/k_2.$
Symulacja silnika w programie typu SPICE
Jesteśmy już gotowi na to, żeby zbudować model silnika DC w LTSpice (a właściwie to w każdym innym programie do symulacji obwodów elektrycznych).
Zrobimy to stopniowo dodając modele kolejnych zjawisk, o których sobie powiedzieliśmy.
Krok 1 - rezystor i cewka
Na początku zamodelujmy wirnik silnika jako rezystor połączony szeregowo z cewką indukcyjną. Odpowiednie parametry można znaleźć np. w kartach katalogowych silników. My w naszym przykładzie użyjemy wartości rezystancji $0.6 \text{ }\Omega$ i indukcyjności $0.3 \text{ mH}$.
Do tego wykonamy symulację typu transient pokazującą co się będzie działo przez pierwsze $10 \text{ ms}$. Założymy, że po $1 \text{ ms}$ od startu symulacji dołączamy do silnika napięcie zasilania $12 \text{ V}$. Odpowiedni schemat znajdziesz na rys. 3.
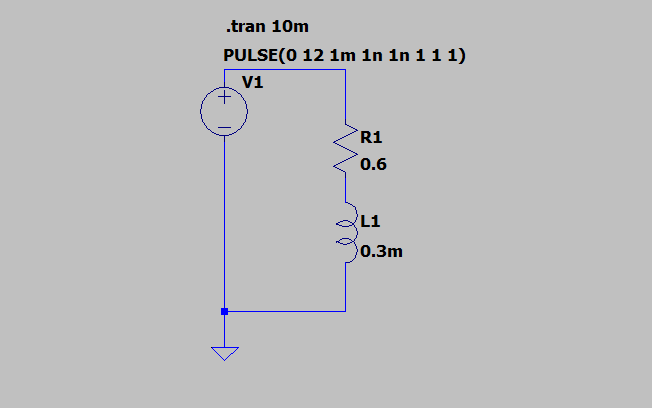
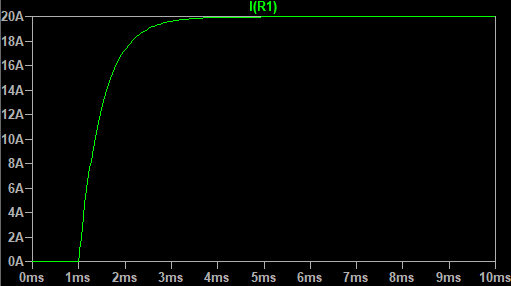
Wynik symulacji znajdziesz na rys. 4. Znajduje się na nim wykres prądu wirnika. Jego wartość dochodzi do $20 \text{ A}$, co wynika wprost z prawa Ohma. Ze względu na indukcyjność prąd nie dochodzi do tej wartości natychmiast, ale dopiero po jakimś czasie.
Krok 2 - prędkość i moment obrotowy
Zanim przejdziemy do modelowania wstecznej siły elektromotorycznej dołączymy do układu model mechaniczny wirnika. Zgodnie z tym co sobie powiedzieliśmy, możemy użyć do tego celu kondensatora.
Napięcie na kondensatorze będzie równe co do wartości prędkości obrotowej wirnika, a jego pojemność – momentowi bezwładności. Moment obrotowy będziemy modelować przez sterowane źródło prądowe, którego prąd będzie proporcjonalny do prądu uzwojenia.
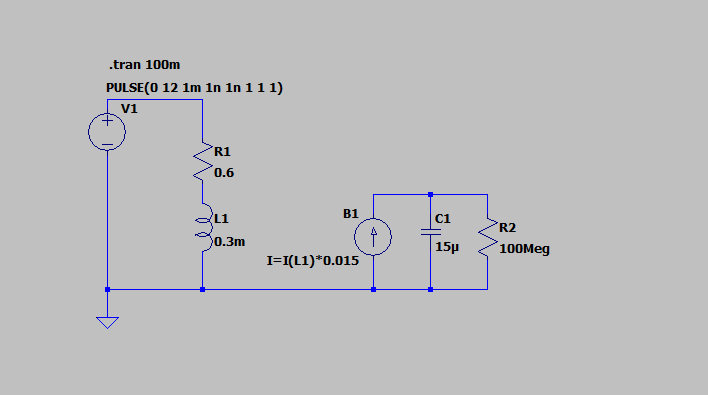
Poprawiony schemat znajdziesz na rys. 5. Jak widzisz użyłem wartości $k_1=0.015 \text{ Nm/A}$ i $I=15 \cdot 10^{-6} \text{ kg} \cdot \text{m}^2$.
Zauważ, że dodałem do układu rezystor o dużej rezystancji. Nie wpływa on na wynik symulacji, ale eliminuje ostrzeżenie zwracane przez symulator.
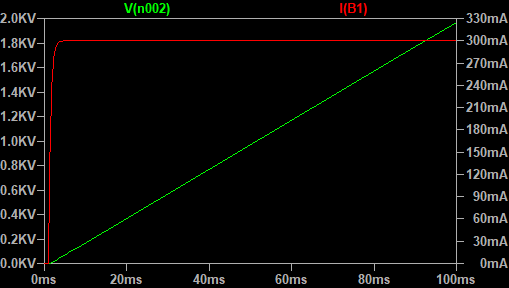
Wynik symulacji (z czasem wydłużonym do $100 \text{ ms}$) znajdziesz na rys. 6. Jak widzisz moment obrotowy dochodzi szybko do wartości $300 \text{ mNm}$ i utrzymuje się na tym poziomie. Zgodnie z drugą zasadą dynamiki taki stały moment powoduje liniowy wzrost prędkości obrotowej. Na rysunku jej wartość dochodzi aż do $1800 \text {rad/s}$. Zwróć uwagę, że zamiast natężenia prądu w amperach odczytujemy wartość momentu w niutonometrach, a zamiast napięcia w woltach – prędkości obrotowej w radianach na sekundę.
Krok 3 - wsteczna siła elektromotoryczna
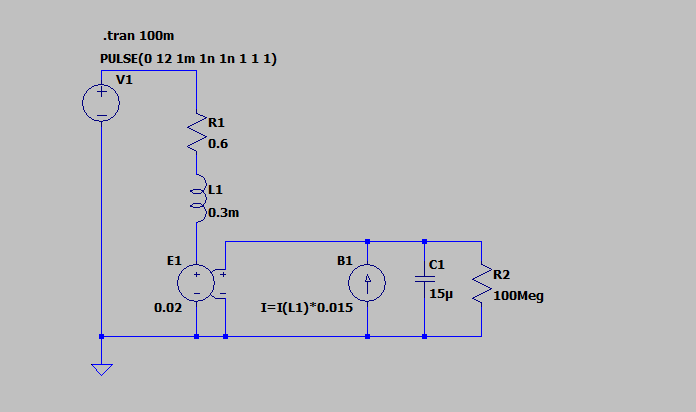
Jak już sobie powiedzieliśmy taki nieograniczony wzrost prędkości obrotowej w silnikach DC nie występuje. Głównym ograniczeniem jest tutaj siła elektromotoryczna. Możemy ją zamodelować dodając do obwodu źródło napięcia sterowane napięciem na kondensatorze. Odpowiedni schemat znajdziesz na rys. 7. Użyłem w nim stałej proporcjonalności między siłą elektromotoryczną, a prędkością obrotową wirnika równą $0.02 \text {V/rad/s}$.
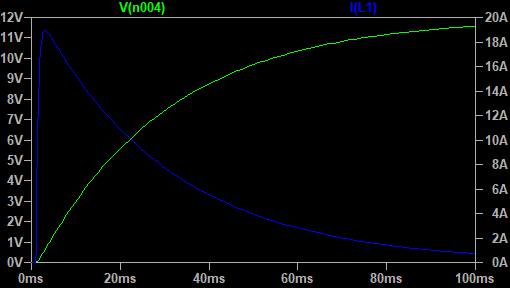
Wynik symulacji przedstawia rys. 8. Zielona linia pokazuje wartość wstecznej siły elektromotorycznej. Zgodnie z tym co pisałem wcześniej, narasta ona aż do wartości napięcia zasilania.
Wzrost siły elektromotorycznej powoduje oczywiście spradek natężenia prądu uzwojenia wirnika. Ponieważ nie modelujemy oporów ruchu to prąd w stanie ustalonym spada aż do zera.
Krok 4 - opory ruchu
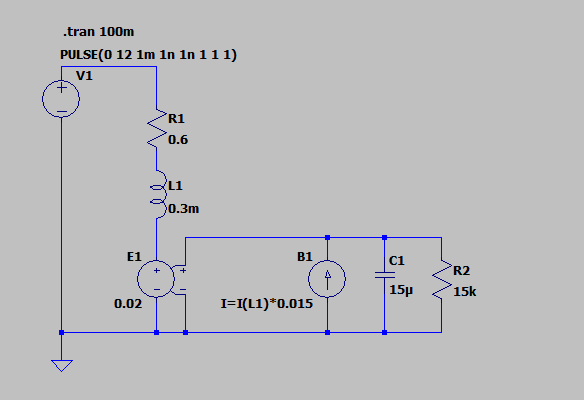
Jak zamodelować opory ruchu silnika? Tak właściwie to nasz schemat zawiera już odpowiedni element. Jest to rezystor $R2$. Aby poprawnie modelować moment hamujący $T_h = \beta \omega$, to wartość tego rezystora musi być równa $1/\beta$.
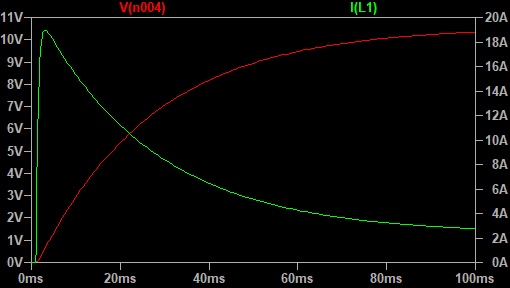
Zwróć uwagę, że im większe opory tym mniejsza rezystancja $R2$. Obecna wartość $100 \text{ M}\Omega$ właściwie nie wprowadza to układu strat energii. Zmniejszmy ją do bardziej realistycznej wartości $15 \text{ k}\Omega$. Zmodyfikowany schemat i wynik symulacji znajdziesz na rys. 9 i 10.
Zwróć uwagę na to, że wsteczna siła elektromotoryczna nie osiąga już wartości $12 \text{ V}$, a prąd uzwojenia zatrzymuje się na wartości około $3 \text{ A}$. Dzięki temu udało nam się w końcu uzyskać realistyczny model pracy silnika.
Podsumowanie
Jak widzisz, poprawne zamodelowanie pracy silnika elektrycznego nie jest takie proste. Należy połączyć ze sobą wiedzę zarówno na temat części elektrycznej jak i mechanicznej silnika.
Mam nadzieję, że ten artykuł pomoże Ci nie tylko w symulacjach obwodów z silnikiem elektrycznym ale też lepiej zrozumieć jak te silniki działają.
No related posts.


2 komentarze do “Symulacja silnika prądu stałego w SPICE”
Pingback: Dioda zabezpieczająca. Przekaźniki dla początkujących cz. 3 - InterTech Academy
Pingback: Dodajemy potencjometr do LTSpice - InterTech Academy