Widzenie maszynowe cz. 4
Detekcja prostych obiektów geometrycznych
Znając już metody detkcji występujących w obrazie krawędzi możemy pójść krok dalej i nauczyć się jak wykrywać obecne w nim proste obiekty geometryczne. Istnieje wiele różnych algorytmów detekcji w obrazach cyfrowych takich obiektów jak punkty, linie, okręgi czy elipsy. My zajmiemy się tzw. transformacją Hougha, której można używać do wykrywania różnych krzywych dających się opisać równaniami matematycznymi. Użyjemy dostępnej w bibliotece scikit-image implementacji transformacji Hougha do detekcji linii prostych i okręgów w przykładowych obrazach.
Notatniki Jupytera i przykładowe obrazy do tego wpisu możesz pobrać klikając w ten link.
Jak działa transformacja Hougha?
Tym razem zamiast się rozpisywać przygotowałem krótki film na temat funkcjonowania transformacji do detekcji linii prostych:
Implementacja w Pythonie
Jak zwykle naszą implementację w Pythonie zaczynamy od importu niezbędnych bibliotek. Do modułów, które już poznaliśmy dodamy tym razem moduł skimage.transform, który zawiera implementację transformacji Hougha:
import numpy as np
import PIL
import matplotlib.pyplot as plt
import skimage.feature
import skimage.transform
Następny krok to wczytanie obrazu, na którym będziemy pracować. Ponieważ jest on kolorowy to najpierw przeprowadzimy też konwersję do skali szarości:
im = np.array(PIL.Image.open('room.jpg'))/255
im = np.mean(im,axis=2)
plt.imshow(im, cmap='gray') 
Teraz za pomocą detektora Canny’ego przeprowadzamy detekcję krawędzi:
im_edge = skimage.feature.canny(im, sigma=3.0, low_threshold=0.02, high_threshold=0.1)
plt.imshow(im_edge) 
Teraz jesteśmy gotowi przeprowadzić transformację Hougha:
angles = np.linspace(0, 180, 181)/180*pi
hough, angles, dist = skimage.transform.hough_line(im_edge, theta=angles)
plt.pcolor(angles*180/np.pi, dist, hough)
plt.clim(vmin=0, vmax=50)
plt.colorbar() 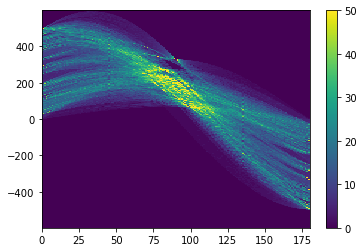
W pierwszym wierszu za pomocą funkcji linspace dostępnej w module numpy generujemy tablicę kątów, dla których chcemy zbudować mapę parametrów linii prostych w obrazie. Funkcja ta generuje nam tablicę 181 równoodległych od siebie wartości od 0 do 180. Będzie to nasza tablica kątów, którą następnie przeliczamy ze stopni na radiany.
W kolejnym kroku wywołujemy funkcję hough_line z modułu skimage.transform. Przyjmuje ona jako argumenty obraz binarny z wykrytymi krawędziami i tablicę kątów. Funkcja zwraca nam krotkę, która zawiera trzy elementy: wartości mapy parametrów, listę kątów i listę odległości od początku układu współrzędnych. Tutaj rozpakowaliśmy te elementy do zmiennych hough, angles i dist.
Na koniec wyświelamy wynik transformacji za pomocą funkcji pcolor z modułu pyplot. Dodatkowo za pomocą funkcji clim ograniczamy skalę kolorów do wartości 50, żeby uzyskać lepszy kontrast na wykresie.
Detekcja prostych
Dysponując transformatą Hougha możemy teraz wykryć proste w obrazie. Zaczynamy od znalezienia lokalnych maksimów w transformacji. Moduł skimage.transform posiada służącą do tego funkcję o nazwie hough_line_peaks.
accum, peak_angles, peak_dist = skimage.transform.hough_line_peaks(hough, angles, dist, threshold=100)
plt.pcolor(angles*180/np.pi, dist, hough)
plt.clim(vmin=0, vmax=50)
plt.colorbar()
plt.scatter(peak_angles*180/np.pi, peak_dist, c='r') 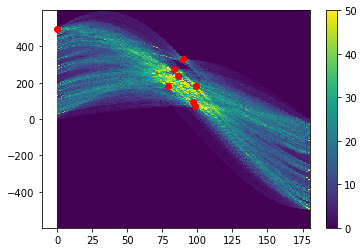
Funkcja przyjmuje jako argumenty wynik transformacji Hougha, tablice kątów i odległości od początku układu współrzędnych oraz wartość progu, który muszą przekroczyć wykryte maksima. Zwracana jest krotka, która zawiera wartości transformacji, kąty oraz odległości dla tych maksimów.
W ostatnim wierszu za pomocą funkcji scatter zaznaczamy wykryte maksima na wykresie.
Na koniec możemy wyświetlić wykryte linie na obrazie:

Detekcja okręgów
Przy pomocy transformacji Hougha możemy wykrywać nie tylko linie proste, ale w teorii dowolnej krzywe opisane pewnymi równaniami matematycznymi. Problem polega na tym, że złożone krzywe zdefiniowane przez wiele parametrów wymagają wielowymiarowych tablic, a przez to czas obliczania transformacji bardzo się wydłuża.
W miarę prostym przykładem do wykrycia są obecne na obrazie okręgi. Okręg jest zdefiniowany przez trzy parametry (dwie współrzędne środka i promień), więc transformacja Hougha ma jeszcze rozsądne rozmiary. Poniżej znajdziesz przykładowy wynik takiej detekcji. Kod użyty do uzyskania tego efektu znajdziesz w notatniku dołączonym do tego wpisu.


