Obliczanie strat energii w tranzystorze MOSFET
W jednym z poprzednich wpisów opisywałem w jaki sposób możemy odprowadzać ciepło generowane w układach elektronicznych pod wpływem przepływającego prądu. Świadome podejmowanie decyzji o tym jakie metody odprowadzenia zastosować wymaga umiejętności oszacowania jakie ilości ciepła będą generowane w projektowanym układzie generowane. Elementami, które często generują duże ilości ciepła są tranzystory MOSFET pracujące jako klucze przełączające prądy o dużych natężeniach. Dlatego w tym artykule zobaczymy w jaki sposób obliczyć straty energii w tranzystorze MOSFET pracującym właśnie jako taki klucz.
Od czego zależy ilość ciepła generowana w elemencie elektronicznym?
Każdy element elektroniczny, przez który przepływa prąd pobiera (lub dostarcza jeżeli mówimy o źródłach energii) pewną ilość energii, która w wielu przypadkach jest całkowicie tracona w postaci ciepła. Szybkość dostarczania tej energii (czyli moc pobierana przez element) jest równa:
$$p = u\cdot i,$$
gdzie $p$ jest mocą, $u$ – napięciem na zaciskach elementu, a $i$ – natężeniem przepływającego prądu.
Zrozumienie tego wzoru ma bardzo duże znaczenia do zrozumienia problemu nagrzewania się elementów elektronicznych. Aby ograniczyć ilość generowanego ciepła należy obniżyć (najlepiej do zera lub prawie do zera) jedną z dwóch wielkości: napięcie na zaciskach elementu lub natężenie przepływającego prądu. Wniosek ten prowadzi wprost do metody zwanej modulacją szerokości impulsu (PWM – pulse width modulation).
Technika PWM
Technikę PWM omówimy na przykładzie sterowania prostym silnikiem prądu stałego. Wyobraź sobie silnik, który zasilany jest z napięcia 12 V i pobiera przy tym prąd o natężeniu 2 A. Dla uproszczenia założymy, że z punktu widzenia obwodu silnik jest po prostu rezystorem o rezystancji 6 omów. Nie jest to do końca prawda, ale to temat na inny artykuł. Wspomnijmy tylko o jednej ważnej różnicy. Uzwojenie silnika posiada silną indukcyjność, która przy nagłym przerwaniu przepływającego przez nią prądu wywoływałaby przepięcia mogące zniszczyć inne elementy obwodu. Dlatego należy do niego równolegle dołączać diodę, która umożliwi stopniowe wygaszenia prądu gdy tranzystor w układzie PWM zostanie nagle odcięty.
Załóżmy teraz, że chcemy sterować silnikiem ograniczając jego prędkość obrotową przez obniżenie napięcia na cewce silnika do 6 V. Jak możemy to zrobić?
Jedną z metod jaką możem sobie wyobrazić polega na tym, żeby dołączyć do silnika szeregowo tranzystor MOSFET, którego bramkę wysterujemy takim napięciem, że efektywna rezystancja kanału tranzystora spowoduje odłożenie się na nim 6 V napięcia. Pozostałe 6 V pozostanie na cewce silnika. Precyzyjne ustawienie odpowiedniego napięcia na bramce wymaga jakiejś formy sprzężenia zwrotnego. Przykładowy układ może wyglądać tak jak na rysunku poniżej. Ten układ nie wymaga dołączonej do silnika diody, gdyż tranzystor nie jest nagle odcinany.
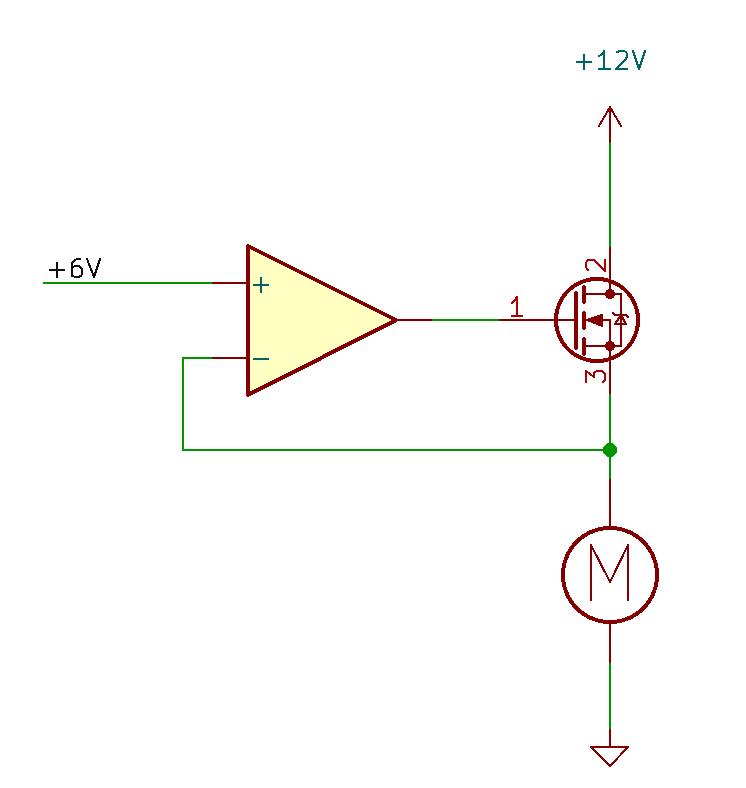
Jaki prąd popłynie w tym układzie? Zakładając, że będzie on proporcjonalny do napięcia na cewce silnika jego natężenie wyniesie 1 A (połowa tego co przy 12 V). Problem polega na tym, że ten sam prąd popłynie też przez tranzystor MOSFET, na którym odkłada się też znaczne napięcie (6 V). Spowoduje to straty mocy na tranzystorze równe 6 W. Zakładając, że nie chcemy nagrzać tranzystora bardziej niż 60 stopni powyżej temperatury otoczenia, dopuszczalna rezystancja termiczna między złączem tranzystora, a otoczeniem wyniesie 10 K/W. Wymaga to już zastosowania zewnętrznego radiatora o wymiarach znacznie większych niż sam tranzystor.
Żeby rozwiązać ten problem wymyślono technikę zwaną modulacją szerokości impulsów – PWM. Polega ona na tym, żeby szybko przełączać tranzystor między stanem całkowitego odcięcia, w którym przez układ w ogóle nie będzie płynął prąd albo stanem całkowitego włączenia, w którym tranzystor będzie miał bardzo niską rezystancję kanału.
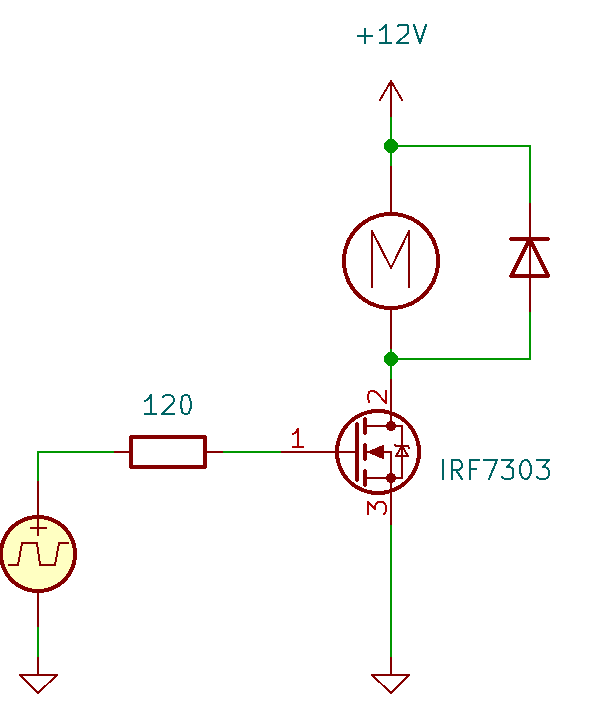
W obu stanach moc rozpraszana na tranzystorze będzie równa lub bardzo bliska zeru. W przypadku odcięcia natężenie prądu będzie równe zeru, a więc o żadnych stratach mocy nie może być mowy. W przypadku pełnego otwarcia między drenem, a źródłem tranzystorem nie będzie prawie żadnego napięcia elektrycznego, a więc pomimo przepływu prądu rozpraszana moc będzie niewielka.
W stanie odcięcia napięcie na cewce silnika wyniesie 0 V, a w stanie pełnego włączenia 12 V. Średnie napięcie na cewce będzie zależało od tego jaki będzie stosunek czasu podczas, które tranzystor przewodzi do całkowitego okresu przełączania. Ten stosunek nazywamy „współczynnikiem wypełnienia”.
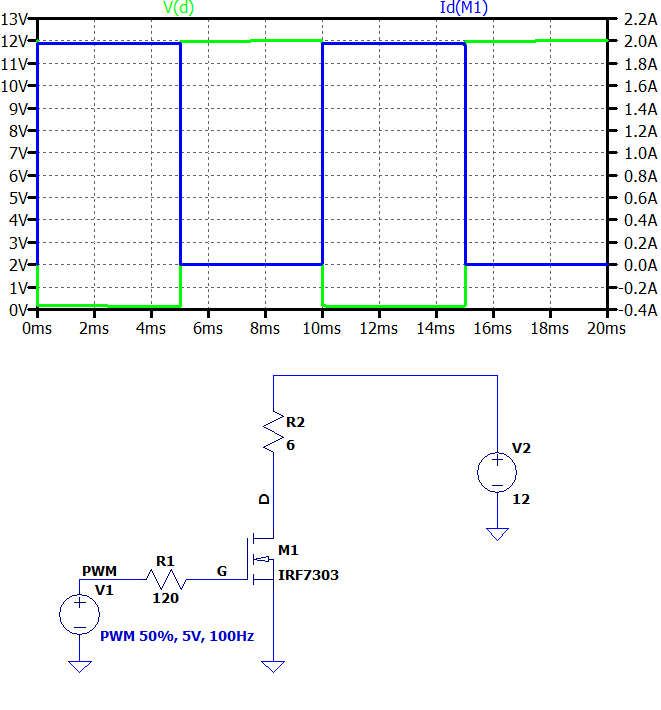
W naszym przykładzie współczynnik wypełnienia 50% da nam średnie napięcie na cewce równe 6 V. Jego zwiększenie do 75% spowodowałoby wzrost średniego napięcia do 9 V.
Czy jednak można tak po prostu posługiwać się średnim napięciem na cewce i zignorować to, że tak naprawdę bardzo szybko przełącza się ono między dwoma stanami? Okazuje się, że tak. Silnik jest elementem mechanicznym obdarzonym pewną bezwładnością. Jeżeli częstotliwość przełączania będzie odpowiednio duża to nie zdąży on reagować na zmiany napięcia i jego działanie będzie nierozróżnialne od tego jakie wystąpiłoby przy podłączaniu napięcia stałego o odpowiedniej wartości.
Straty mocy na podczas przewodzenia tranzystora
Niestety tranzystor nie zachowuje się jak idealny przełącznik i nawet w stanie pełnego włączenia ma pewną rezystancję. W notach katalogowych tranzystorów MOSFET oznacza się ją jako Rds(on). Pod wpływem prądu o natężeniu $i$ spowoduje to na tranzystorze spadek napięcia o wartości:
$$u = i \cdot R_{\text{DS(on)}}.$$
Należy użyć tutaj prądu, który pojawi się przy podłączeniu do obciążenia pełnego napięcia zasilania (w naszym przykładzie 2 A). Dalej będziemy ten prąd oznaczać jako $i_\text{max}$.
Mnożąc to napięcie przez natężenie prądu dostaniem wzór na traconą na tranzystorze moc:
$$p = i_{\text{max}}^2 \cdot R_{\text{DS(on)}}.$$
Spróbujmy wykonać przykładowe obliczenia. Dla tranzystora IRF7303 rezystancja Rds(on) wynosi 0.08 oma przy napięciu bramka-źródło równym 5 V. Jeżeli maksymalny prąd obciążenia wynosi 2 A to moc tracona na tranzystorze w formie ciepła wyniesie 320 mW. Jest to wartość na tyle niewielka, że tranzystor będzie mógł pracować bez radiatora. Rezystancja termiczna złącze-otoczenie dla tego typu tranzystorów wynosi 60 K/W, a więc temperatura tranzystora wzrośnie o ok. 20 stopni względem temperatury otoczenia.
Warto też zwrócić uwagę, że taka moc wydzieli się tylko przy ciągłym włączeniu tranzystora. W rzeczywistości trzeba ją pomnożyć przez współczynnik wypełnienia impulsów. Często interesuje nas jednak najgorszy przypadek, a więc ten, który analizowaliśmy.
Straty mocy podczas przełączania tranzystora
Niestety straty powstałe podczas przewodzenia tranzystora mogą okazać się nie być głównym źródłem ciepła w układzie. Otóż, kiedy tranzystor przechodzi ze stanu włączenia do stanu odcięcia przez moment musi on przejść przez stan pośredni, w którym odkłada się na nim zarówno duże napięcia jak i przepływa przez niego duży prąd.
Energia, która jest rozpraszana przez tranzystor w formie ciepła może być oszacowana z poniższego wzoru (jest on ważny dla obciążeń indukcyjnych – w przypadku obciążeń rezystancyjnych będzie ona nieco niższa):
$$E = \frac{1}{2} u_{\text{zas}} \cdot i_{\text{max}} \cdot \Delta t,$$
gdzie $u_{\text{zas}}$ to napięcie zasilania układu, a $\Delta t$ to czas przełączania tranzystora. Wielkość $i_{\text{max}}$ oznacza prąd maksymalny (nie średni) prąd obciążenia, czyli taki jaki powstanie przy podłączenia do niego pełnego napięcia zasilania.
Ponieważ energia $E$ jest tracona dwukrotnie podczas każdego cyklu (podczas włączania i wyłączania) to moc strat będzie równa:
$$p = 2Ef = u_{\text{zas}}i_{\text{max}}f\Delta t$$
Oznacza to, że im większa będzie częstotliwość przełączania tym większe będą straty mocy. Jest to jeden z powodów, dla którego nie należy zwiększać ponad potrzebę częstotliwości sygnału PWM.
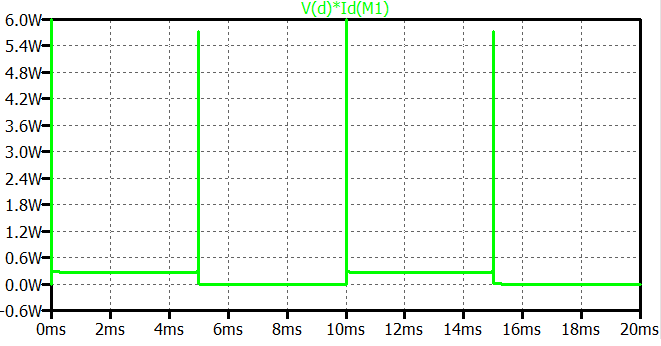
Obliczanie czasu przełączania tranzystora
Kluczowe dla obliczenia strat energii na przełączanie tranzystora jest oszacowanie czasu potrzebnego na przełączenie tranzystora. Czas ten jest zależny od dwóch czynników: pierwszym jest ładunek elektryczny, który należy doprowadzić/odprowadzić od bramki tranzystora aby go włączyć/wyłączyć, a drugim wydajność prądowa źródła, którym sterujemy bramkę.
Początkujący elektronicy często sądzą, że bramka tranzystora MOSFET nie przewodzi prądu. Jest to prawda, ale tylko jeżeli chodzi o prąd stały. Włączenie tranzystora wymaga doprowadzenia do bramki pewnej ilości ładunku elektrycznego. Wyłączenie tranzystora wymaga z kolei odprowadzenie tego ładunku. Oba te procesy wymagają przepływu prąd elektrycznego.
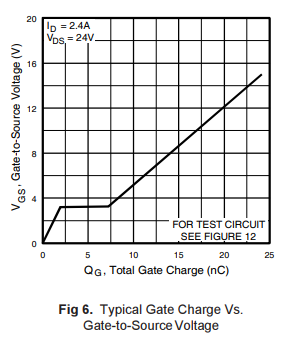
Aby obliczyć czas przełączania musimy najpierw wyznaczyć potrzebną ilość ładunku. Można ją odczytać z noty katalogowej tranzystora z wykresu przypominającego ten z rysunku poniżej. Proces przełączania tranzystora MOSFET jest trochę skomplikowany i nie mamy tu miejsca żeby go dokładnie opisać. W każdym razie możemy odczytać, że doprowadzenie do bramki tranzystora IRF7303 napięcia 5 V, przy którym zaczyna on przewodzić wymaga ok. 8 nC ładunku elektrycznego.
Załóżmy, że chcemy sterować bramką tranzystora z portu GPIO mikrokontrolera o wydajności prądowej 40 mA. Taki prąd włączy tranzystor w czasie :
$$\Delta t = 8 \text{nC} / 40 \text{mA} = 200 \text{ns}.$$
Niestety założenie, że prąd ładowania bramki będzie cały czas wynosił 40 mA jest nieco nierealistyczne. W praktyce w tego typu układach między port GPIO, a bramkę tranzystora powinniśmy włączyć rezystor, który ograniczy prąd do 40 mA (czyli 5 V/40 mA = 125 omów). W przeciwnym razie przy dużej częstotliwości przełączania prąd bramki tranzystora mógłby uszkodzić porty mikrokontrolera.
W tego typu konfiguracji prąd 40 mA popłynie tylko na początku procesu włączania/wyłączania tranzystora, gdy napięcie między bramką a portem GPIO jest równe 5 V. W miarę postępów przełączania napięcia to będzie malało, a z nim i prąd. W praktyce trzeba więcej zwiększyć czas przełączania mniej więcej 2 razy. W naszym przykładzie będzie to oznaczać, że tranzystor będzie się włączał i wyłączał w czasie około 400 ns.
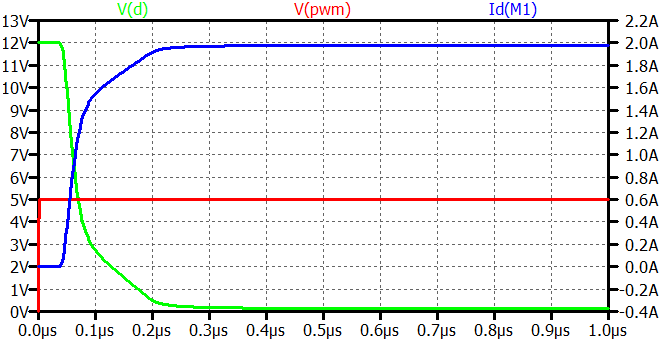
Wróćmy teraz do naszego przykładu. Przy napięciu zasilania 12 V nasz silnik pobiera 2 A prądu. Tranzystor przełącza się w czasie 1 mikrosekundy, a więc energia wytracona jako ciepło podczas każdego przełączenia to:
$$E = \frac{1}{2} \cdot 12 \text{V} \cdot 2 \text{A} \cdot 400 \text {ns} = 4,8 \mu\text J.$$
Jeżeli częstotliwość sygnału PWM ustawimy na 100 Hz to otrzymamy moc strat na przełączanie:
$$p = 2 \cdot 4,8 \mu \text J \cdot 100 \text{Hz} = 0,96 \text{mW}.$$
Jak widać jest to pomijalnie mała wartość. Zawdzięczamy to przede wszystkim niskiej częstotliwości przełączania. Taka wartość jest w porządku dla sterowania silnikami prądu stałego, ale może być dużo za niska dla takich zastosowań jak np. zasilacze impulsowe. W tego typu zasilaczach stosuje się zwykle częstotliwości rzędu 100 kHz, co pozwala stosować cewki o niskich indukcyjnościach (rzędu 10 mikrohenrów). Jak jednak widzisz może to wygenerować już duże straty mocy podczas przełączania tranzystora. Rozwiązaniem jest tutaj stosowanie dedykowanych układów scalonych do sterowania bramką tranzystorów MOSFET, które pozwalają szybko włączyć lub wyłączyć tranzystor.
Podsumowanie - obliczanie strat mocy na tranzystorze MOSFET pracującym jako klucz
Podsumujmy wszystko co do tej pory ustaliliśmy w formie krótkiej procedury szacowania strat mocy traconej w formie ciepła na tranzystorach MOSFET pracujących jako klucz:
- Ustalamy wymagania projektowe: napięcie zasilania $u_{\text{zas}}$ i prąd obciążenia przy podłączeniu pełnego zasilania $i_{\text{max}}$, częstotliwość sygnału PWM $f$ i wydajność prądową źródła sterującego bramką $i_{G}$.
- Po doborze tranzystora odczytujemy jego rezystancję w stanie włączenia $R_{\text{DS(on)}}$ oraz ładunek elektryczny, który trzeba doprowadzić do bramki podczas włączania – $Q$.
- Obliczamy straty mocy na tranzystorze w czasie przewodzenia: $p_1 = i_{\text{max}}^2R_{\text{DS(on)}}$.
- Obliczamy czas przełączania tranzystora $\Delta t = 2 \cdot Q/i_{G}$.
- Obliczamy straty mocy na przełączanie: $p_2 = u_{\text{zas}} \cdot i_{\text{max}} \cdot \Delta t \cdot f$.
No related posts.


2 komentarze do “Obliczanie strat energii w tranzystorze MOSFET”
Dobrze napisany artykuł.
Proszę mi wytłumaczyć dlaczego wyliczone „delta t ” (ze wzoru wynika, że jest to stała czasowa) trzeba zwiększyć dwa razy skoro przyjmuje się, że kondensator jest naładowany w pełni w czasie 5 x stała czasowa. W tym wypadku stała czasowa wynosi 200ns, czyli czas ładowania wynosi 1 us.
Pięciokrotność stałej czasowej to raczej przesadne oszacowanie. Po upływie dwóch stałych czasowych kondensator ładuje się do prawie 90% swojej pojemności co zwykle oznacza, że tranzystor jest już otwarty.