Decybele - o co w nich chodzi?
Zajmujesz się elektroniką? Prędzej czy później będziesz musiał się zetknąć ze skalą decybelową. Jeżeli jeszcze się to nie stało, albo zdarzyło Ci się natknąć na te tajemnicze „decybele” i do końca rozumiesz o co w nich chodzi to ten wpis jest właśnie dla Ciebie. Przeczytaj go koniecznie bo zrozumienie pojęcia decybeli jest niezbędne, żeby na poważnie zajmować się elektroniką (i zresztą nie tylko elektroniką).
Gdzie można się natknąć na decybele?
W elektronice decybele pojawiają się głównie przy opisie różnego rodzaju wzmacniaczy i filtrów, czyli układów, których zadaniem jest wzmacnianie lub tłumienie sygnałów elektrycznych. Na pewno prędzej czy później natkniesz się na takie sformułowania jak np.:
- wzmocnienie wynosi 20 dB (decybeli),
- filtr ma tłumienie rosnące o 20 dB na dekadę.
Jak należy to rozumieć? Zanim do tego dojdziemy to powiedzmy sobie bardzo ważną rzecz na temat decybeli.
Decybele to jednostka względna
Najważniejsza rzecz jaką musisz zrozumieć jest to, że decybele (dB) to jednostka względna. Np. zdanie, że „napięcie jest równe 20 dB” nie ma żadnego sensu. Brakuje w nim poziomu odniesienia. Widać to zwłaszcza wyraźnie w przypadku opisu właśnie wzmacniaczy. Jeżeli powiemy, że wzmacniacz ma wzmocnienie równe 3 dB to znaczy, że poziom sygnału na jego wyjściu jest większy o 3 dB od poziomu napięcia na wejściu.
Tak więc nie mówimy, że coś ma np. 5 dB, ale że coś jest o 5 dB większe albo mniejsze od czegoś innego. Czasami można dodać ten poziom odniesienia do skrótu dB tworząc np. jednostkę „dBm”, o której pisałem Ci w przykładzie z mocą nadajnika. O tym też porozmawiamy później dokładnie.
Skala logarytmiczna i definicja decybela
Wyobraź sobie, że mamy dwa napięcia: $U_1$ i $U_2$. Stosunek tych napięć wyrażony w decybelach definiuje się jako logarytm dzisiętny z ich ilorazu pomnożony przez 20:
$k[dB] = 20 \log {\frac{U_2}{U_1}}.$
Warto nauczyć się kilku przykładów na pamięć:
| $U_1/U_2$ | $k [dB]$ |
|---|---|
| 0.1 | -20 |
| 0.5 | -6 |
| 1 | 0 |
| $\sqrt{2}$ | 3 |
| 2 | 6 |
| 10 | 20 |
| 100 | 40 |
Policzmy jakiś przykład. Jeżeli $U_1$ wynosi 2 V, a $U_2$ 4 V, to zgodnie z naszą tabelą $U_2$ jest o 6 dB wyższe niż $U_1$.
Kilka zasad obliczeniowych
Zasada 1. Mnożenie wzmocnień odpowiada dodawaniu decybeli.
Jeżeli np. napięcie $U_1$ jest równe 1 V, a napięcie $U_2$ 200 V to ich stosunek wynosi 46 dB. Dlaczego właśnie 46 dB? Liczbę dwieście możemy zapisać jako $100 \cdot 2$. 100 to w skali decybelowej 40, a 2 to 6. Dodając do siebie te dwie wartości otrzymujemy 46 dB. Płyną z tego np. dwa ważne wnioski:
- każde podwojenie napięcia $U_2$ powoduje zwiększenie $k$ o 6 dB,
- każde dziesięciokrotne zwiększenie $U_2$ powoduje wzrostu $k$ o 20 dB.
Spójrz, że skala decybelowa „spłaszcza” stosunki między napięciami. Np. wzmocnienia równe kolejno 10, 100 i 1000 to w skali decybelowej 20 dB, 40 dB i 60 dB.
Zasada 2. Zamiana mnożenia na dzielenie zmienia znak w skali decybelowej
To bardzo prosta zasada. Jeżeli $U_2$ jest np. 20 razy większe niż $U_1$ to ich stosunek wynosi 26 dB. Jeżeli zaś $U_2$ byłoby 20 razy mniejsze niż $U_1$ to ich stosunek wynosiłby -26 dB.
Zasada 3. Podniesienie stosunku do kwadratu podwaja liczbę decybeli.
Np. jeżeli wzmocnienie równe 4 to 12 dB (policz samodzielnie), to wzmocnienie równe 16 da nam 24 dB.
Po co nam to wszystko?
Decybele przydają się, żeby operować na wielkościach, które mogą się zmieniać o kilka rzędów wielkości. Wyobraź sobie prosty układ rezonansowy z cewką, kondensatorem i rezystorem. Zróbmy symulację takiego układu w programie LTSpice (rys. 1).
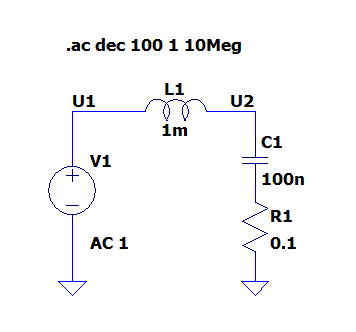
Napięcie w punkcie U2 zależy mocno od częstotliwości. Dla częstotliwości rezonansowej może być ono dużo wyższe niż napięcie ze źródła sygnału (U1), a dla wysokich częstotliwości – dużo niższe. Wyobraź sobie, że chcielibyśmy teraz pokazać na jednym wykresie jak wartość U2 zmienia się z częstotliwością sygnału zakładając, że amplituda napięcia U1 to 1 V. W LTSpice służy do tego symulacja AC, która da nam taki wykres.
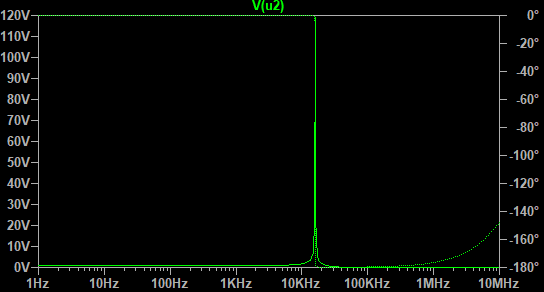
Czy potrafisz z tego wykresu odczytać ile wynosi wartość U2 dla częstotliwości 1 Hz albo 1 MHz? Nie da się tego zrobić gdyż proporcje między tymie wartościami, a wartością w rezonansie (120 V) są zbyt duże.
Ale jeżeli narysujemy zamiast tego stosunek U2 do U1 w decybelach to otrzymamy taki wykres:
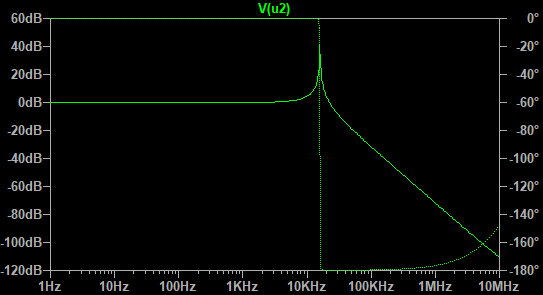
I teraz wszystko jest jasne. Napięcie U2 dla częstotliwości 1 Hz jest o 0 dB większe od U1, czyli wynosi 1 V. Dla częstotliwości 1 MHz ich stosunek wynosi mniej więcej -70 dB. Napięcie U2 jest więc około 2000 razy niższe niż U1 (1/2000 to -67 dB). Będzie to więc wartość rzędu 0.5 mV. Dzięki decybelom wartości, które różnią się aż tak znacznie przedstawiliśmy na jednym wykresie.
Decybele i moc
Tutaj dochodzimy do bardzo ważnej sprawy. W decybelach podawaliśmy stosunki dwóch napięć. Oczywiście można też podawać stosunki dwóch natężeń prądów. Definicja jest tutaj dokładnie taka sama. Inaczej sprawa wygląda jednak jeżeli będziemy podawać stosunek dwóch mocy. Jeżeli mamy dwie moce $P_1$ i $P_2$ to ich stosunek $P_2/P_1$ wyrażony w decybelach jest zdefiniowany jako:
$k [dB] = 10 \log {\frac{P_2}{P_1}},$
czyli połowa tego, co mielibyśmy dla takiego samego stosunku napięć.
Dlaczego tak jest? Moc wydzielana na elementach rezynstancyjnych zwiększa się mniej z kwadratem płynącego przez nie prądu albo z kwadratem przyłożonego napięcia. Czyli podwojenie napięcia na rezystorze zwiększy czetery razy wydzielaną na nim moc.
Wyobraź sobie teraz, że do wyjścia wzmacniacza o wzmocnieniu napięciowym 6 dB podłączamy jakiś rezystor. Napięcie na rezystorze jest 2 razy większe gdybyśmy podłączyli go do wejścia wzmacniacza.
A gdybyśmy zapytali się teraz nie o wzmocnienie napięć ale wzmocnienie mocy? Moc na rezystorze podpiętym do wyjścia będzie 4 razy większa niż moc na rezystorze podpiętym do wejścia. Gdybyśmy zostawili „napięciową” definicję decybeli to musielibyśmy powiedzieć, że wzmocnienie wzmacniacza to nie 6 dB, ale 12 dB. Żeby tego uniknąć umówiono się, że podając stosunek napięć (albo natężeń prądu) logartym mnożymy razy 20, a podając stosunek mocy – razy 10. Dzięki temu zawsze powiemy, że nasz wzmacniacz ma wzmocnienie 6 dB.
Podsumowanie
Jeżeli to Twój pierwszy kontakt z decybelami to nie wszystko jest pewnie dla Ciebie jasne. Nie martw się – każdy kto dzisiaj biegle używa tych jednostek przez to przechodził. Za jakiś czas posługiwanie się decybelami będzie dla Ciebie bardzo prostą i wygodną czynnością.
No related posts.


4 komentarze do “Decybele. O co w nich chodzi?”
Na liście mailingowej jest biała czcionka na białym tle. Trudno się zapisać (;
W tabeli nie powinno czasem byc U2/U1?
Czegoś tutaj nie zrozumiałem. W pierwszym przykładzie U2/U1 (4V/2V) = 2 zatem to 6dB a nie 2 dB… ?
Słusznie – wkradł się mały błąd. Powinno być oczywiście 6 dB. Już poprawiłem.